Binary tree

full binary tree

A binary tree in which each node has exactly zero or two children is called a full binary tree. In a full tree, there are no nodes with exactly one child.


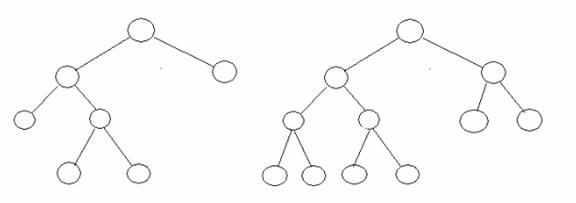
如果二叉樹中除了葉子節點（leaf node），每個節點的度都為2，則此二叉樹稱為滿二叉樹。

什么是二叉树，二叉树及其性质详解

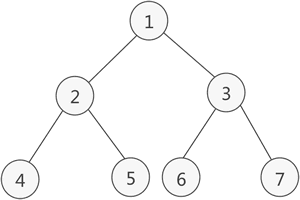
complete binary tree

A complete binary tree is a tree, which is complete filled, with the possible exception of the bottom level, which is filled from left to right. A complete binary tree of the heigher h has between 2^h and 2^(h+1)-1 nodes.

Tree Data Structure


如果二叉樹中除去最後一層節點為滿二叉樹，且最後一層的節點依次從左到右分佈，則此二叉樹稱為完全二叉樹。

什么是二叉树，二叉树及其性质详解

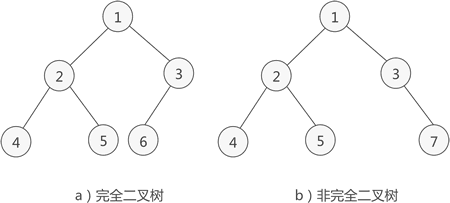
perfect binary tree

  • 滿二叉樹（Full binary tree）：除去葉節點，每個節點都有兩個子節點。
  • 完全二叉樹（Complete binary tree）：除去最深一層之外，其餘所有層的節點都必須有兩個子節點，且最深一層的節點均集中在左邊，即左對齊。
  • 完美二叉樹（Perfect binary tree）：滿足完全二叉樹性質，樹的葉子節點均在最後一層（形成一個完美的三角形）

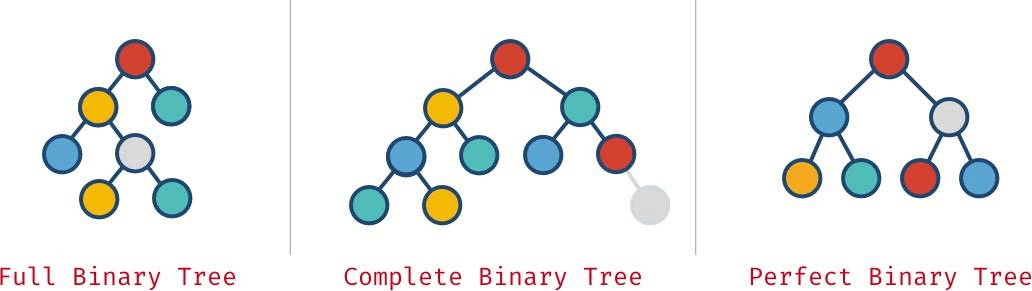
滿二叉樹、完全二叉樹、完美二叉樹並不總是互斥的：

  • 完美二叉樹必然是滿二叉樹和完全二叉樹：
    • 完美二叉樹正好有2^k-1個節點，其中k是樹的最深一層（從1開始）。
  • 完全二叉樹並不總是滿二叉樹：
    • 正如上面的完全二叉樹例子，最右側的灰色節點是它父子點僅有的一個子節點。如果移除掉它，這棵樹就既是完全二叉樹，也是滿二叉樹。 （注：其實有了那個灰色節點的話，這棵樹不能算是完全二叉樹，因為滿二叉樹需要左對齊）
  • 滿二叉樹並不一定是完全二叉樹與完美二叉樹。

Binary search tree

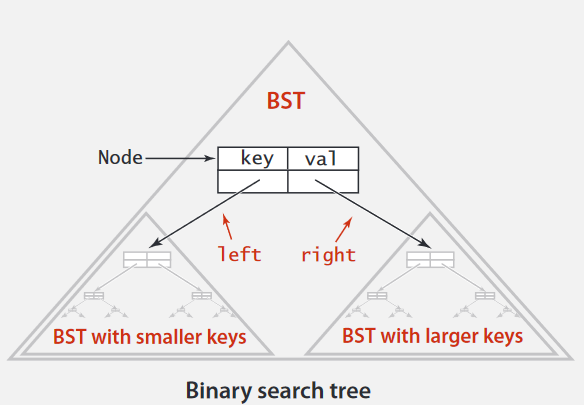
A binary search tree (BST) is a binary tree where each node has a Comparable key (and an associated value) and satisfies the restriction that the key in any node is larger than the keys in all nodes in that node’s left subtree and smaller than the keys in all nodes in that node’s right subtree.

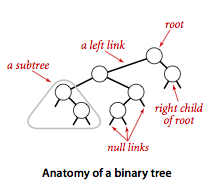
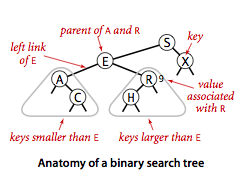
Basic implementation

Source: BST.java

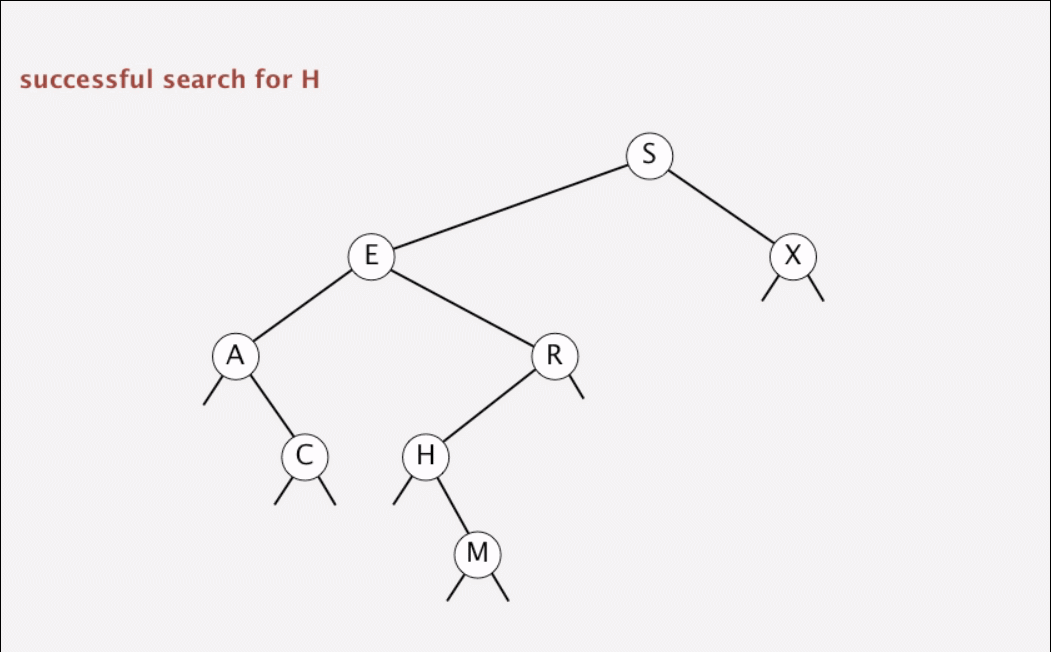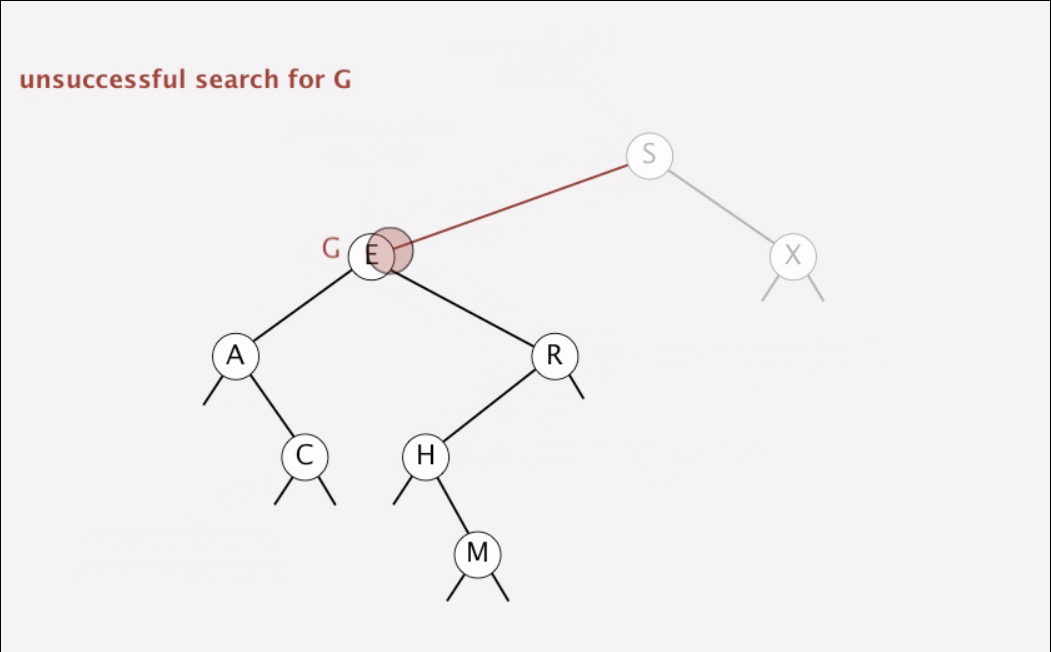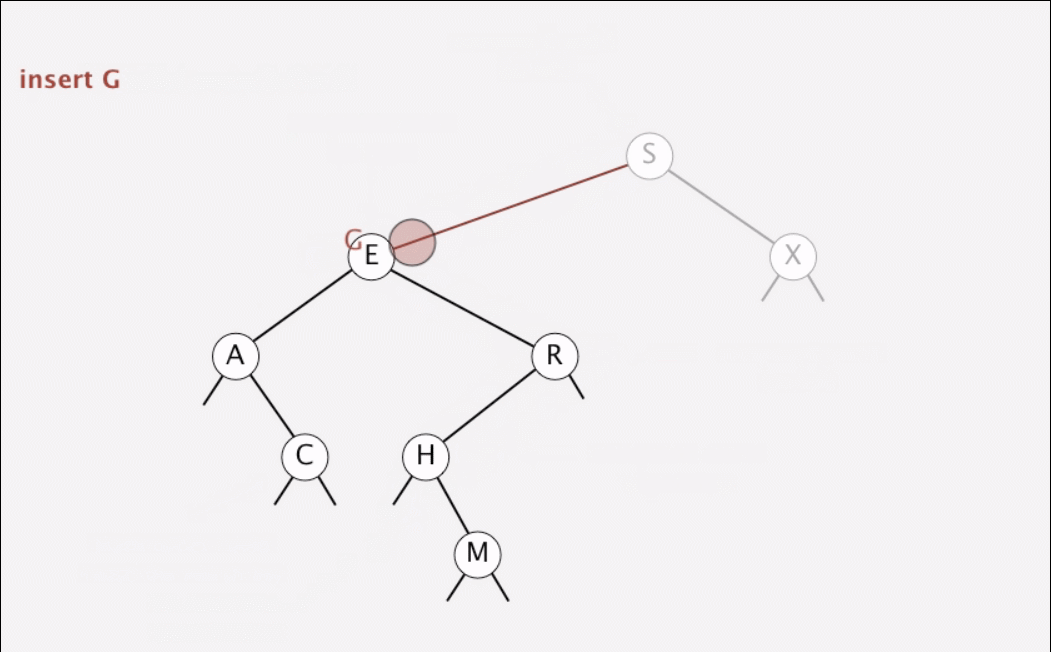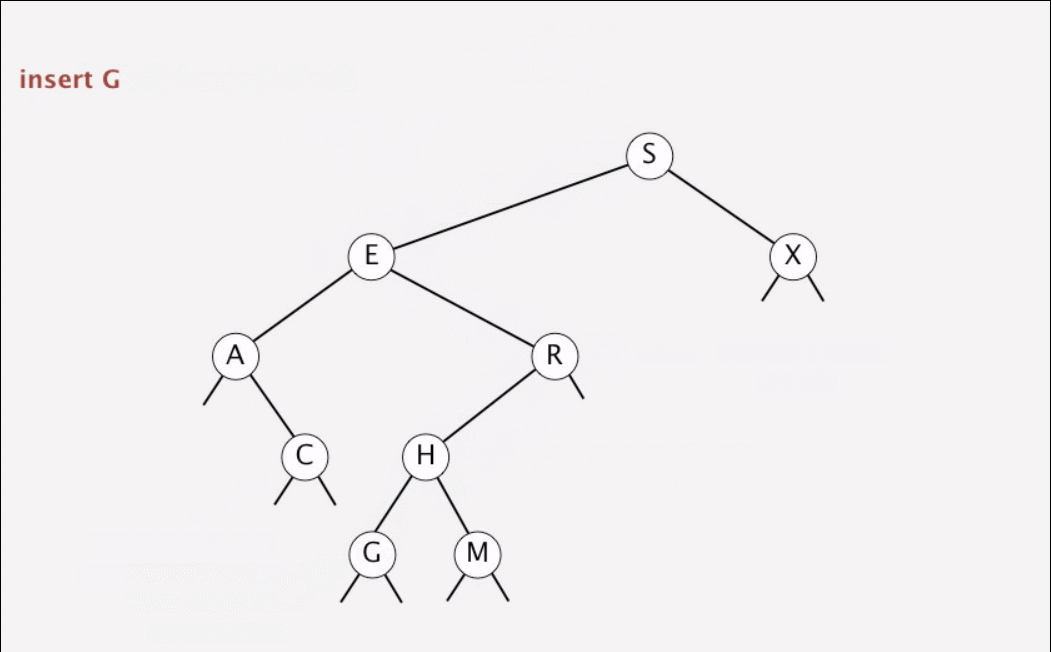
A recursive algorithm to search for a key in BST follow immediately from the recursive structure: If the tree is empty, we have a search miss; if the search key is equal to the key at the root, we have a search hit. Otherwise, we search (recursively) in the appropriate subtree. The recursive get() method implements this algorithm directly. It takes a node (root of a subtree) as first argument and a key as second argument, starting with the root of the tree and the search key.


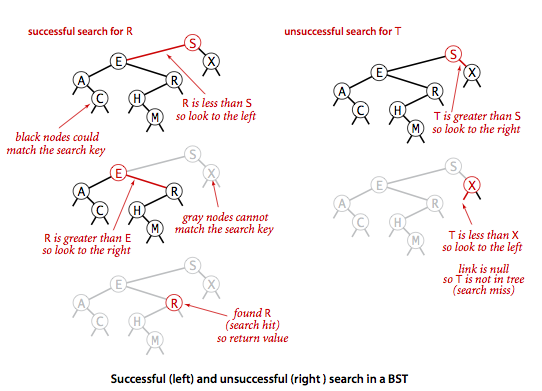
思路：

  • 將當下parent node與tree root node比值，得出-1（小於）、1（大於）或是0（等於）
  • 如果找到，返回，否則繼續使用遞歸算法，持續求解
/**
 * Returns the value associated with the given key.
 *
 * @param key the key
 * @return the value associated with the given key if the key is in the symbol table
 * and {@code null} if the key is not in the symbol table
 * @throws IllegalArgumentException if {@code key} is {@code null}
 */
public Value get(Key key) {
    return get(root, key);
}

private Value get(Node x, Key key) {
    if (key == null) throw new IllegalArgumentException("calls get() with a null key");
    if (x == null) return null;
    int cmp = key.compareTo(x.key);
    if      (cmp < 0) return get(x.left, key);
    else if (cmp > 0) return get(x.right, key);
    else              return x.val;
}

insert

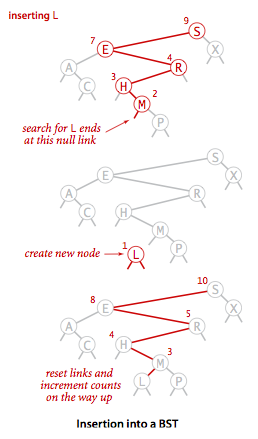
Insert is not much more difficult to implement than search. Indeed, a search for a key not in the tree ends at a null link, and all that we need to do is replace that link with a new node containing the key. The recursive put() method accomplishes this task using logic similar to that we used for the recursive search:

  • If the tree is empty, we return a new node containing the key and value;
  • if the search key is less than the key at the root, we set the left link to the result of inserting the key into the left subtree;
  • otherwise, we set the right link to the result of inserting the key into the right subtree.

思路：

不斷的遞歸搜索左右孩子，知道找到一個null節點，就把<key, value>插入。 如果key本身在樹中，則更新值。

插入操作可以用遞歸來做。（凡是涉及鏈表的插入操作，都可以考慮用遞歸，如果用非遞歸相對來說麻煩點， 因為插入操作是在父節點上插入一個左右各半的孩子節點，如果root為空還得單獨判斷）

/**
 * Inserts the specified key-value pair into the symbol table, overwriting the old 
 * value with the new value if the symbol table already contains the specified key.
 * Deletes the specified key (and its associated value) from this symbol table
 * if the specified value is {@code null}.
 *
 * @param  key the key
 * @param  val the value
 * @throws IllegalArgumentException if {@code key} is {@code null}
 */
public void put(Key key, Value val) {
    if (key == null) throw new IllegalArgumentException("calls put() with a null key");
    if (val == null) {
        delete(key);
        return;
    }
    root = put(root, key, val);
    assert check();
}

private Node put(Node x, Key key, Value val) {
    if (x == null) return new Node(key, val, 1);
    int cmp = key.compareTo(x.key);
    if      (cmp < 0) x.left  = put(x.left,  key, val);
    else if (cmp > 0) x.right = put(x.right, key, val);
    else              x.val   = val;
    x.size = 1 + size(x.left) + size(x.right);
    return x;
}


動畫演示：

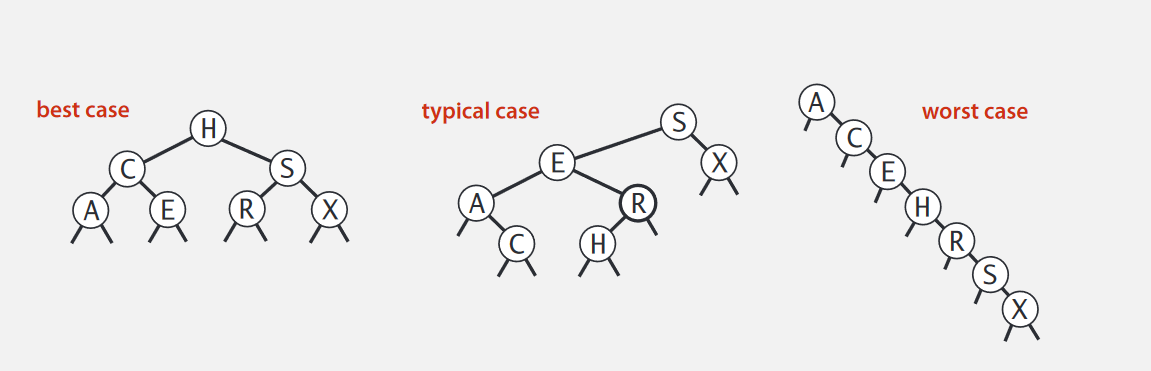
Analysis

根據不同的插入順序，二叉樹會呈現出不同的形狀，最好的狀態當然是完全平衡的狀態，這個時候搜索效率最高， 最壞的形式就是插入的序列有序，這個時候二叉樹的搜索效率就是N了。


這個隨機插入的效果：


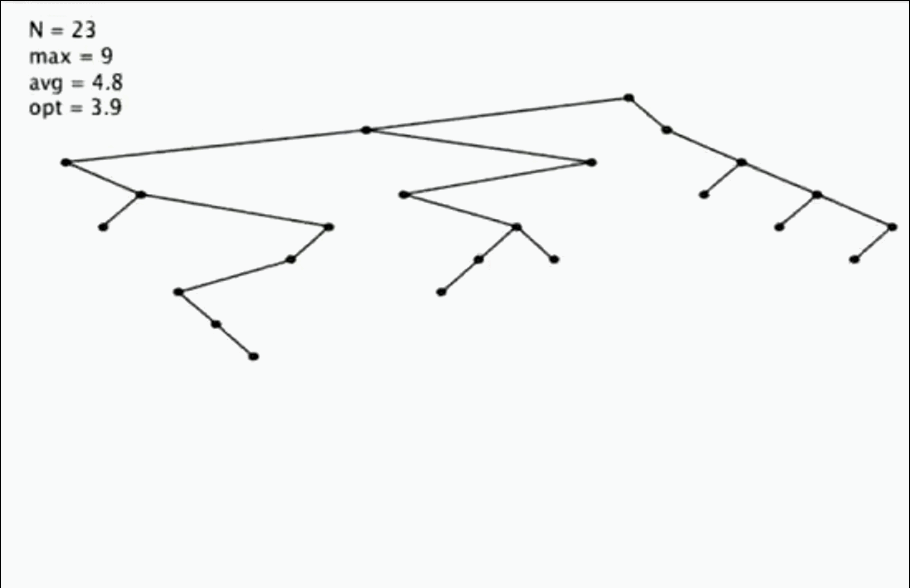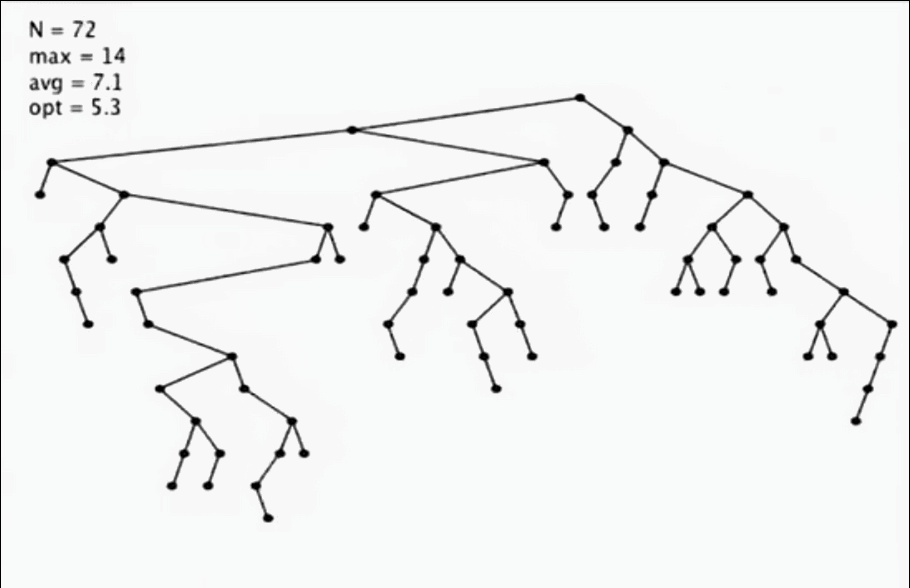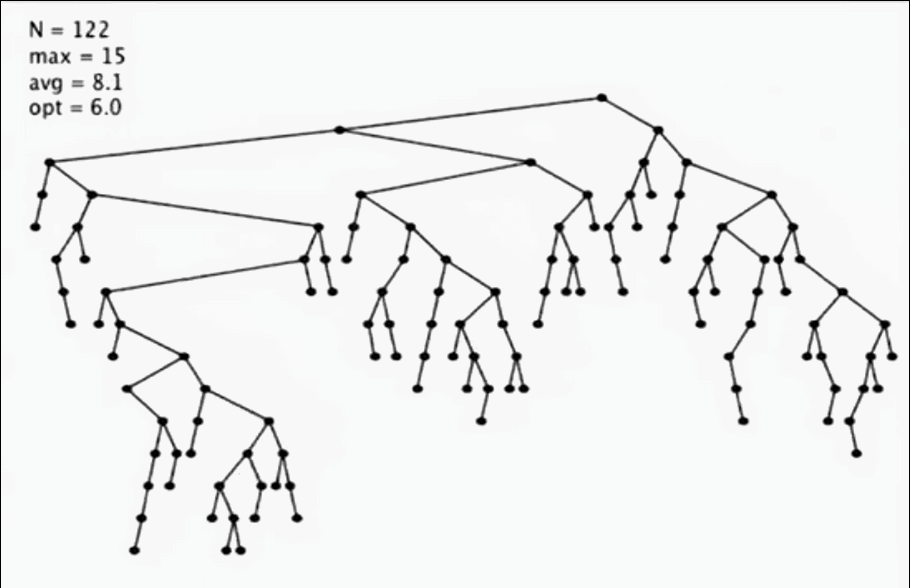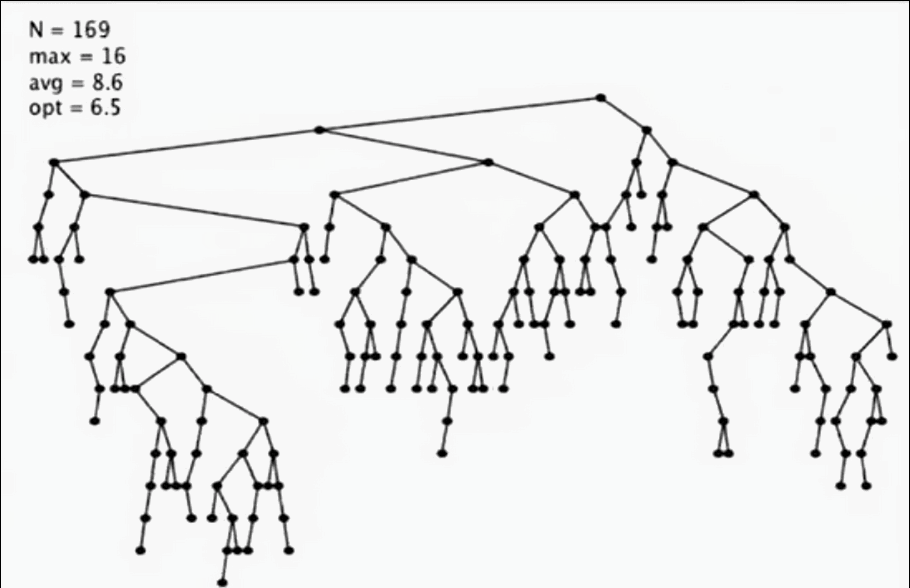
研究表明，如果插入是隨機的情況下，二叉樹的平均深度都不深。所以通常二叉樹的效率還是很高的。

Order-based methods

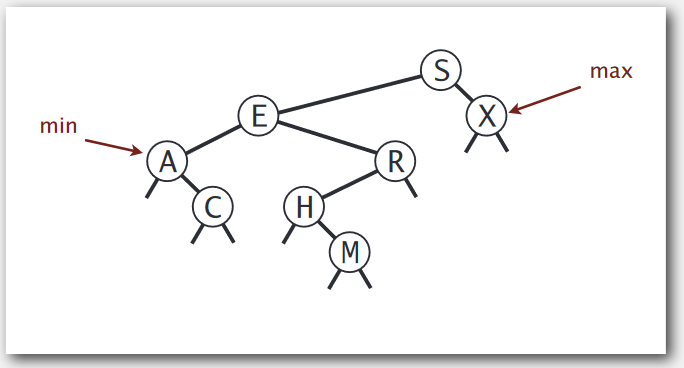
minimum and maximum

這個很簡單，最小的話直接搜索到最左的孩子，最大的話直接搜索到最右的孩子。

p.s. 搜索到意思就代表用遞歸算法來實現

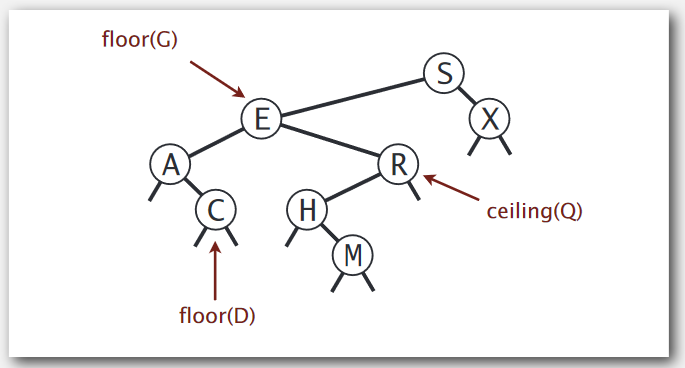
floor and ceiling

floor：找到比key小的最大key
ceiling：找到比key大的最小key

selection

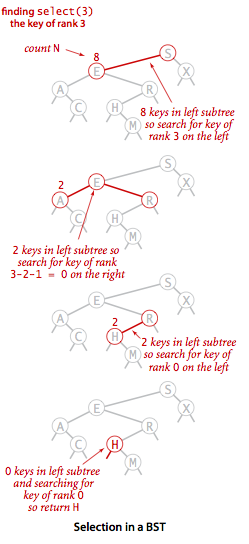
Suppose that we seek the key of rank k (the key such that precisely k other keys in the BST are smaller). If the number of keys t in the left subtree is larger than k, we look (recursively) for the key of rank k in the left subtree; if t is equal to k, we return the key at the root; and if t is smaller than k, we look (recursively) for the key of rank k - t - 1 in the right subtree.

假設我們尋找等級為k 的密鑰（該密鑰使得BST中的其他k個密鑰恰好較小）。 如果左子樹中的鍵數t大於k，我們將（遞歸）尋找左子樹中等級k的鍵；如果t等於k，則返回根的鍵； 如果t小於k，我們（遞歸）在右邊的子樹中尋找等級k-t-1的關鍵字。

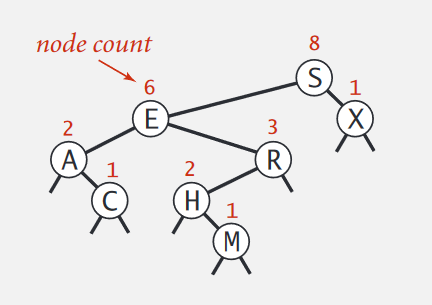
rank

返回鍵小於key的個數。有三種情況：

  • root == key：左孩子count（因為只有左孩子小於它）
  • root < key：左孩子count + 1（自己）+ 右孩子繼續找
  • root > key：左孩子繼續找（給定key還沒找到比自己小的）

delete

根據二叉樹的結構，很簡單了：

  • 遍歷左子樹
  • 把自己key插入列隊
  • 遍歷右子樹
public Iterable<Key> keys() {
    Queue<Key> q = new Queue<Key>();
    inorder(root, q);
    return q;
}

private void inorder(Node x, Queue<Key> q) {
    if (x == null) return;
    inorder(x.left, q);
    q.enqueue(x.key);
    inorder(x.right, q);
}

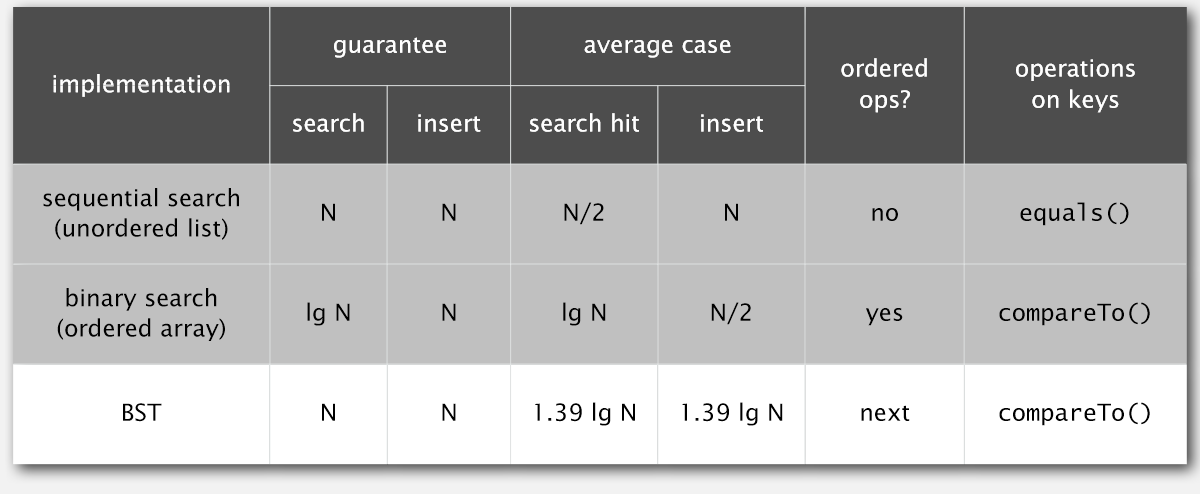
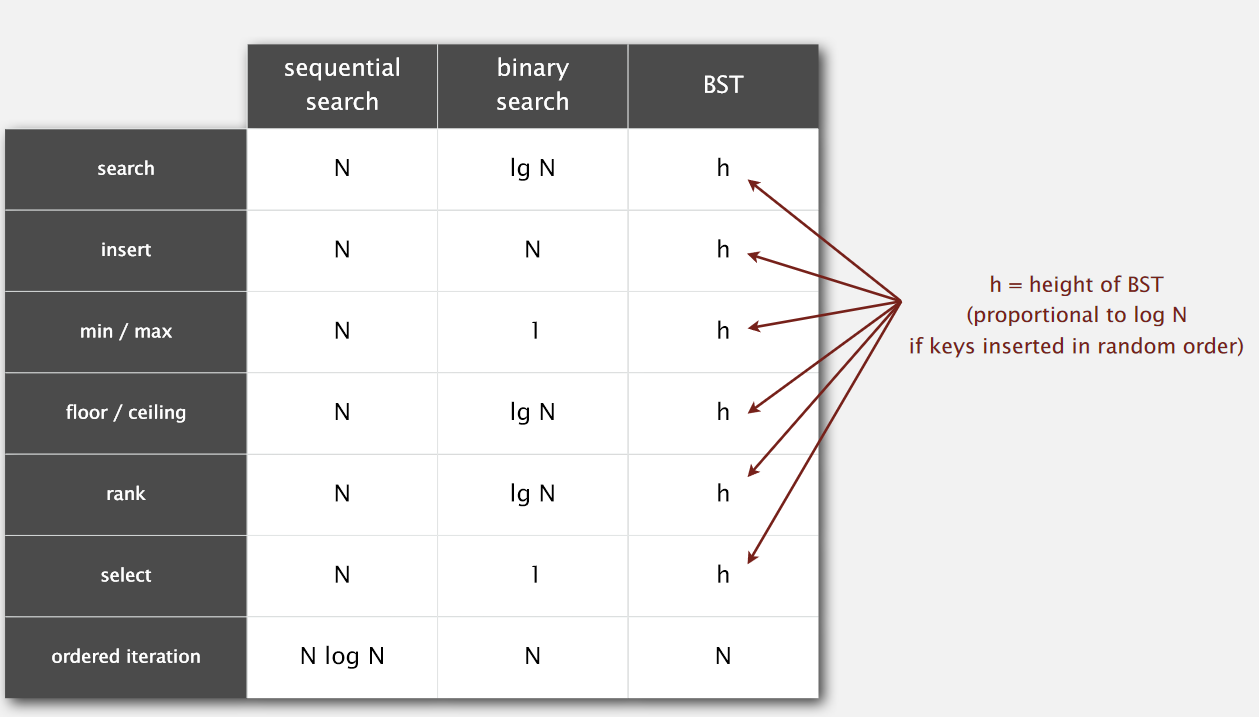
Operations summary

用二叉樹實現的符號表操作，其時間複雜度要遠遠小於其他方式。

LeetCode

花花酱 LeetCode Binary Trees 二叉树 - 刷题找工作 SP12

create a BST

public class TreeNode {
    private int val;
    private TreeNode left;
    private TreeNode right;
    private TreeNode root;

    public TreeNode() {
    }

    public TreeNode(int val) {
        this.val = val;
    }

    public TreeNode(TreeNode node, int val) {
        this.val = val;
        node.left = null;
        node.right = null;
    }

    public TreeNode createBST(List<Integer> nums) {
        root = new TreeNode();
        for (Integer num : nums)
            root = insert(root, num);

        return root;
    }

    public TreeNode insert(TreeNode root, int val) {
        if (root == null) return new TreeNode(val);

        if (val <= root.val) root.left = insert(root.left, val);
        else               root.right = insert(root.right, val);

        return root;
    }

    public boolean search(TreeNode root, int x) {
        if (root == null) return false;
        if (root.val == x) return true;

        if (root.val < x) return search(root.left, x);
        else            return search(root.right, x);
    }

    public boolean balanced(TreeNode root) {
        if (root == null) return true;
        return Math.abs(height(root.left) - height(root.right)) <= 1 && balanced(root.left) && balanced(root.right);
    }

    public int height(TreeNode root) {
        if (root == null) return 0;

        int l = height(root.left);
        int r = height(root.right);
        return Math.max(l, r) + 1;
    }

    public void preOrder(TreeNode root) {
        if (root == null) return;

        print(root.val);
        preOrder(root.left);
        preOrder(root.right);
    }

    public void inOrder(TreeNode root) {
        if (root == null) return;

        inOrder(root.left);
        print(root.val);
        inOrder(root.right);
    }

    public void postOrder(TreeNode root) {
        if (root == null) return;

        postOrder(root.left);
        postOrder(root.right);
        print(root.val);
    }

    public int maxVal(TreeNode root) {
        if (root == null) return 0;

        int maxLeft = maxVal(root.left);
        int maxRight = maxVal(root.right);
        int maxLR = Math.max(maxLeft, maxRight);
        return Math.max(root.val, maxLR);
    }

    public void print(int val) {
        System.out.print(val + "\t");
    }
}

recursion key

Example: find the max val of a tree

  • Traditional way:
ans = -inf
func maxVal(root):
  ans = -inf;
  traverse(root)
  return ans

func traverse(root):
  if not root: return
  ans = max(ans, root.val)
  traverse(root.left)
  traverse(root.right)
  • Recursive way:
func maxVal(root):
  if not root: return -inf
  max_left = max(root.left)
  max_right = max(root.right)
  return max(root.val, max_left, max_right)

templates

  • Template 1: one root
func sovle(root):
  if not root: return ...
  if f(root): rturn ...
  
  l = solve(root.left)
  r = solve(root.right)
  
  return g(root, l, r)
  • LC 104. Maximum Depth of Binary Tree
func maxDepth(root):
  if not root: return 0
  
  l = maxeDepth(root.left)
  r = maxeDepth(root.right)
  
  return max(l, r) + 1
  • LC 111. Minimum Depth of Binary Tree
func minDpeth(root):
  // if tree is empty (null)
  if not root: return 0
  
  // both left tree and right tree are empty
  if not root.left and not root.right: return 1
  
  l = minDepth(root.left)
  r = minDepth(root.right)
  
  // if left or right tree encounter null node, return current value + 1 (root)
  if not root.left return 1 + r
  if not root.right return 1 + l
  
  return max(l, r) + 1
  • LC 112. Path Sum
func pathSum(root, sum):
  if not root： return false
  if not root.left and not root.right: return root.val == sum
  l = pathSum(root.left, sum - root.val)
  r = pathSum(root.right, sum - root.val)
  return l or r

Applications

Reference