Algorithms - Stacks and Queues
以下資料整理自:
Algorithms, Part I by Princeton University. Week 2: Stacks and Queues
其他參看資料:
BAGS, QUEUES, AND STACKS
Stacks and Queues
Fundamental data types.
- Value: collection of objects.
- Operations: insert, remove, iterate, test if empty.
- Intent is clear when we insert.
- Which item do we remove?
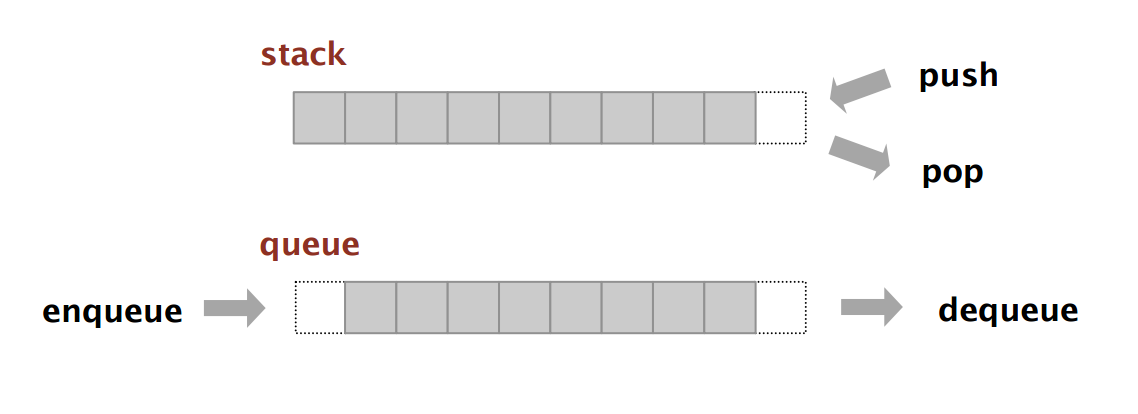
Stack. Examine the item most recently added. ← LIFO = “last in first out”
Queue. Examine the item most recently added. ← FIFO = “first in first out”
Client, implementation, interface
Separate interface and implementation.
Ex: stack, queue, bag, priority queue, symbol table, union-find, ….
Benefits.
- Client can’t know details of implementation → client has many implementation from which to choose.
- Implementation can’t know details of client needs → many clients can re-use the same implementation.
- Design: creates modular, reusable libraries.
- Performance: use optimized implementation where it matters.
Client: program using operations defined interface.
Implementation: actual code implementing operation.
Interface: description of data type, basic operations.
stacks
Stack API
Warmup API. Stack of strings data type.
publci class StackOfStrings
---
StackOfStrings() // create an empty stack
void push(String item) // insert a new string onto stack
String pop() // remove and return the string most recently added
boolean isEmpty() // is the stack empty?
int size() // number of strings on the stack
Warmup client. Reverse sequence of strings from standard input.
Stack test client
Read strings from standard input.
- If string equals “-“, pop string from stack and print.
- Otherwise, push string onto stack.
public static void main(String[] args) {
StackOfStrings stack = new StackOfString();
while (!StdIn.isEmpty()) {
String s = StdIn.readString();
if (s.equals("-")) StdOut.print(stack.pop());
else stack.push(s);
}
}
% more tobe.txt
to br or not to - be - - that - - - is
% java StackOfStrings < tobe.txt
to be not that or be
Stack: linked-list representation
- push
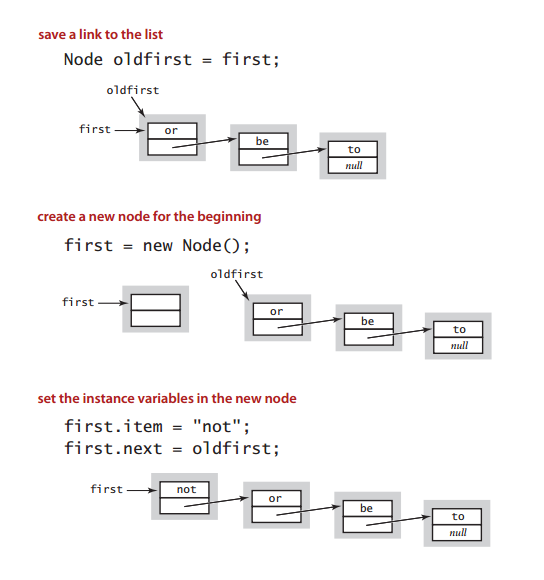
- pop
Stack: linked-list implementation in Java
public class LinkedStackOfStrings {
private Node first = null;
private class Node {
String item;
Node next;
}
public boolean isEmpty() {
return first == null;
}
public void push(String item) {
Node oldFirst = first;
first = new Node();
first.item = item;
first.next = oldFirst;
}
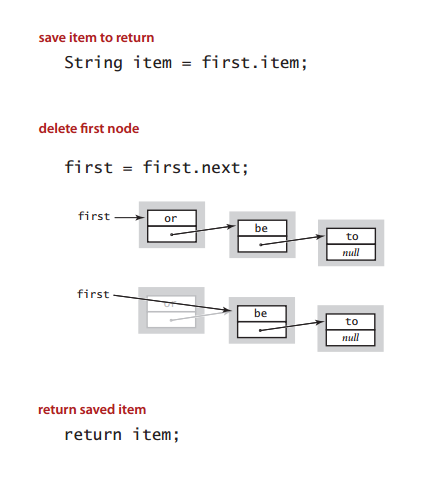
public String pop() {
String item = first.item;
first = first.next;
return item;
}
}
Stack array implementation
Array implementation of a stack.
- Use array s[] to store N items on stack
- push(): add new item at s[N]
- pop(): remove item from s[N-1]
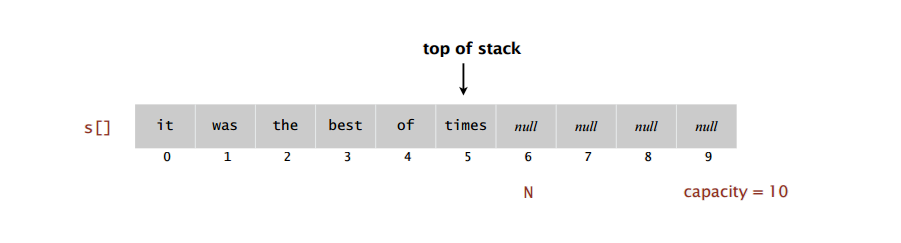
Defect. Stack overflows when N exceeds capacity. [stay tuned]
public class FixedCapacityStackOfStrings {
private String[] s;
private int N = 0;
/**
* constructor
*
* @param capacity a cheat (stay tuned)
*/
public FixedCapacityStackOfStrings(int capacity) {
s = new String[capacity];
}
public boolean isEmpty() {
return N == 0;
}
public void push(String item) {
// use to index into array;
// then increment N
s[N++] = item;
}
public String pop() {
// decrement N;
// then use to index into array
return s[--N];
}
}
Stack considerations with array implementation
Overflow and underflow.
- Underflow: throw exception if pop from an empty stack.
- Overflow: use resizing array for array implementation. [stay tuned]
Null items. We allow null item to be inserted.
Loitering. Holding a reference to an object when it is no longer needed.
public String pop() {
return s[--N];
}
loitering
public String pop() {
String item = s[--N];
s[N] = null;
return item;
}
this version avoids “loitering”:
garbage collector can reclaim memory
only if no outstanding references
We need to pass the size of the array. This violates the idea of the stack which says it should be able to grow and shrink at any size. That’s why stacks not usually implement using a fixed size array.
Stack analysis - linked list vs arrays
Proposition. Every operation takes constant time in the worst case.
Proposition. A stack with N items uses ~ 40 N bytes.
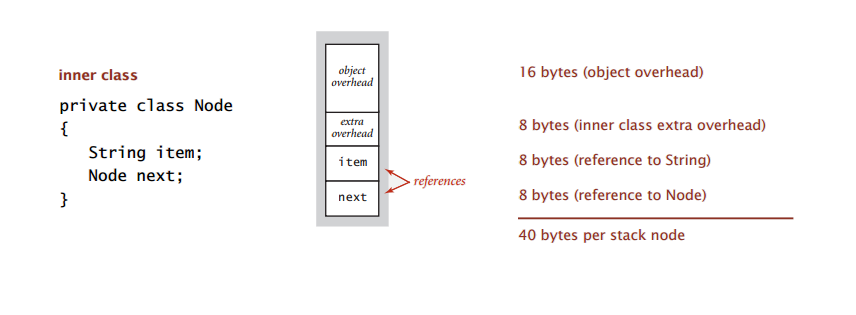
Time → With linked List, the methods takes constant time, but it’s still not that efficient due to object declaration and dealing with links.
While with arrays, accessing the arrays is much faster; It takes O(1).
Memory → Linked Lists requires more memory because of the size of node objects. While with arrays it requires less memory space.
Queues
Queue API
public class QueueOfStrings
---
QueueOfStrings() // create an empty queue
void enqueue(String item) // insert a new string onto queue
String dequeue() // remove and return the string least recently added
boolean isEmpty() // is the queue empty?
int size() // number of strigns on the queue

Queue: linked-list representation
- enqueue
- dequeue
Queue: linked-list implementation in Java
public class LinkedQueueOfStrings {
private Node first, last;
private class Node {
String item;
Node next;
}
public boolean isEmpty() {
return first == null;
}
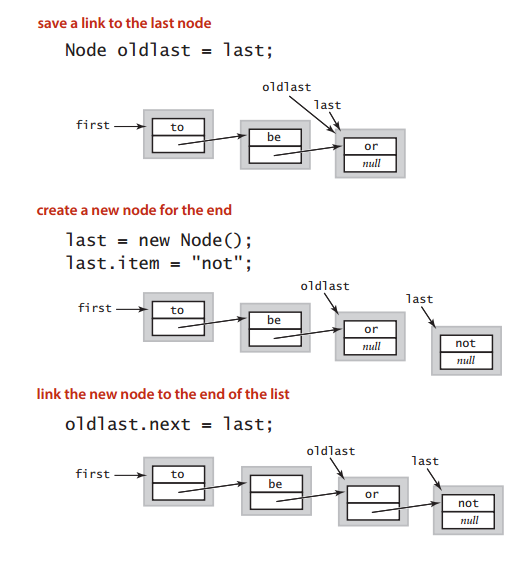
public void enqueue(String item) {
Node oldlast = last;
last = new Node();
last.item = item;
last.next = null;
if (isEmpty()) first = last;
else oldlast.next = last;
}
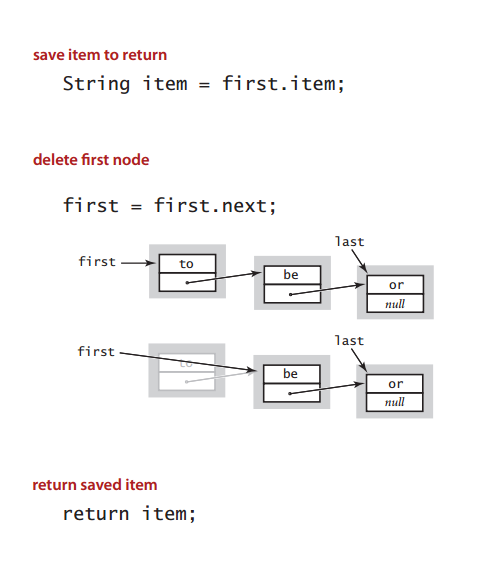
public String dequeue() {
String item = first.item;
first = first.next;
if (isEmpty()) last = null;
return item;
}
}
Queue array implementation
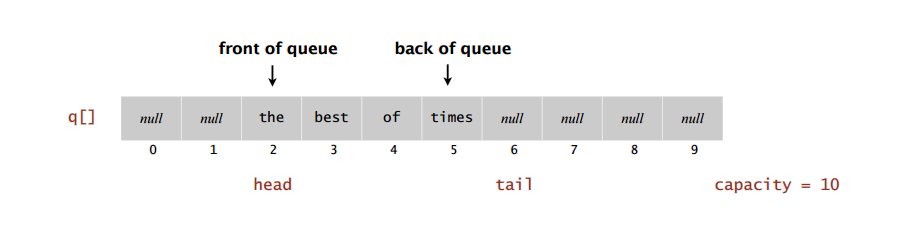
The queue class has an array of values (maybe integers, strings, …), an integer N that represents the number of items in the array.
In addition to two integers, “head” (or first); points to the first inserted node in the array, and “tail” (or last); points to after the last inserted node.
Initially “head” and “tail” points to the first item in the array.
public class ArrayQueue {
private String[] queue;
private int N = 0, head = 0, tail = 0;
public ArrayQueue(int capacity) {
queue = new String[capacity]; // a cheat to keep it simple for now
}
// enqueue an item
public void enqueue(String item) {
queue[tail++] = item;
N++;
}
// dequeue (and return) the first inserted item
public String dequeue() {
String item = queue[head++];
N--;
return item;
}
// is the array empty
public boolean isEmpty() {
return N == 0;
}
}
We need to pass the size of the array. This also violates the idea of the queue (same as with stacks)
Queue wrap-around array
What if “tail” point to the end of the array, while array still have some null values (head is at index 6 for example). The next time we enqueue an item “tail” pointer wil overflow! The same goes for “head” pointer. Both can overflow (as they move to the right), although array may still have empty slots.
So, one way to solve wrap-around, meaning, whenever any pointer overflow (equals to array size), we reset it (point it to the first item in the array).
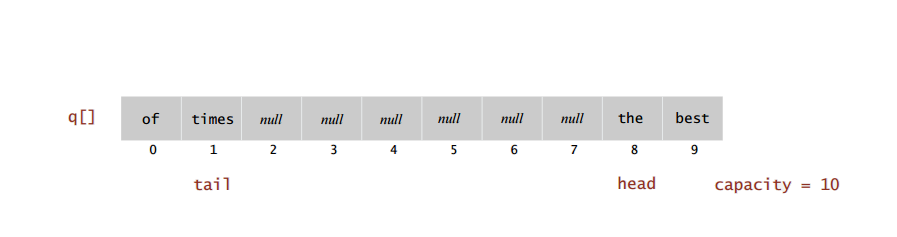
public void enqueue(String item) {
queue[tail++] = item;
N++;
if (tail == queue.length) tail = 0; // wrap-around
}
public String dequeue() {
String item = queue[head++];
N--;
if (head == queue.length) head = 0; // wrap-around
return item;
}
Queue consideration with array implementation
It’s the same consideration already mentioned with Stack.
- Overflow & Underflow: We did not consider the situation when we insert in an item in a full queue, or remove an item from an empty queue.
- Null items: In this case, we allow user to insert null items.
- Loitering: We did not clear reference to objects that are no longer needed.
public String dequeue() {
String item = queue[head];
queue[head++] = null; // avoid loitering
N--;
if (head = queue.length) head = 0;
return item;
}
Queue analysis - linked list vs arrays
Time → It’s same as with Stack using Linked Lists and Arrays.
Memory → It’s also same as with Stack using Linked Lists and Arrays. It just requires additional memory for the two pointers.
Resizing Arrays
Applications
Stack Applications
- Parsing in a compiler.
- Java virtual machine.
- Undo in a word processor.
- Back button in a Web browser.
- PostScript language for printers.
- Implementing function calls in a compiler.
Given a string containing just the characters ( ), { }, [ ], determine if the input string is valid.
An input string is valid if:
Open brackets must be closed by the same type of brackets. Open brackets must be closed in the correct order. Note that an empty string is also considered valid.